1 基于RBF的三维网格重建

假设已有三维物体曲面S上的N个点的点云数据集SP，以及每个点对应的法向量的集合SN，则一阶多项式隐式曲面函数f\left(p\right)可表达为：

f\left(p\right)=\sum_{i=1}^N\;w_i\phi(\parallel p-p_i\parallel)+R(p)=0

其中，p为物体曲面上任意一点，w_i为i点处径向基函数的权重，ϕ(x)表示径向基核函数，||p||表示三维欧式距离，R(p)为一阶多项式R(p)=a+bx+cy+dz。其中w_i和一阶多项式系数a，b，c，d为待求的未知参数。

除了原始点之外，还需要根据原始点的曲面法向量生成离面约束点。其中外部约束点为原始点沿对应曲面法向量位移ε个法向量单位，其对应的约束值为负值；内部约束点为原始点沿对应曲面法向量反位移ε个法向量单位，其对应的约束值为正值；而原始的点位于曲面上，其对应的约束值为0。

这三类约束点以及其对应的约束值满足：

f\left(p\right)=\sum_{j=1}^N\;w_j\phi(\parallel p-p_j\parallel)+R(p_j)=m_i

其中m_i为i点对应的约束值。
且隐式曲面函数式f(p)同时满足正交条件：

\overset N{\underset{j=1}{\sum\;}}w_j=\sum_{j=1}^N\;w_j\;p_j^x\;=\sum_{j=1}^N\;w_j\;p_j^y\;\;=\sum_{j=1}^N\;w_j\;p_j^z\;=0

设\phi_{ij}=\phi(p_i-p_j),则上述公公式可联立为以下方程组：

\left[{\begin{array}{cccccccc}\phi_{11}&\phi_{12}&\dots&\phi_{1N}&1&p_1^x&p_1^y&p_1^z\\\phi_{21}&\phi_{22}&\dots&\phi_{2N}&1&p_2^x&p_2^y&p_2^z\\\vdots&\vdots&\ddots&\vdots&\vdots&\vdots&\vdots&\vdots\\\phi_{N1}&\phi_{N2}&\dots&\phi_{NN}&1&p_N^x&p_N^y&p_N^z\\1&1&\cdots&1&0&0&0&0\\p_1^x&p_2^x&\cdots&p_N^x&0&0&0&0\\p_1^y&p_2^y&\cdots&p_N^y&0&0&0&0\\p_1^z&p_2^z&\cdots&p_N^z&0&0&0&0\end{array}}_{}\right]\begin{bmatrix}w_1\\w_2\\\vdots\\w_3\\a\\b\\c\\d\end{bmatrix}=\begin{bmatrix}m_1\\m_2\\\vdots\\m_4\\0\\0\\0\\0\end{bmatrix}

设：

A=\left[{\begin{array}{cccccccc}\phi_{11}&\phi_{12}&\dots&\phi_{1N}&1&p_1^x&p_1^y&p_1^z\\\phi_{21}&\phi_{22}&\dots&\phi_{2N}&1&p_2^x&p_2^y&p_2^z\\\vdots&\vdots&\ddots&\vdots&\vdots&\vdots&\vdots&\vdots\\\phi_{N1}&\phi_{N2}&\dots&\phi_{NN}&1&p_N^x&p_N^y&p_N^z\\1&1&\cdots&1&0&0&0&0\\p_1^x&p_2^x&\cdots&p_N^x&0&0&0&0\\p_1^y&p_2^y&\cdots&p_N^y&0&0&0&0\\p_1^z&p_2^z&\cdots&p_N^z&0&0&0&0\end{array}}_{}\right]
B=\begin{bmatrix}w_1&w_2&\dots&w_N&a&b&c&d\end{bmatrix}^T
C=\begin{bmatrix}m_1&m_2&\dots&m_N&0&0&0&0\end{bmatrix}^T

通过求解AB=C线性方程组，即可求得未知系数矩阵B，将B回代，即可得到基于RBF的三维曲面函数式。

2 重建思路

令人头疼的理论环节终于过去了，转为正题。
有人就会问？我如何从这些算法理论中重建出一个三维网格模型呢？

  • 首先，你得有一个三维点云数据，并且你知道了每一个点的法向量，这其中会涉及到法向量估计算法，这部分我会在后续的博文中进行讲述。
  • 然后，你需要按照第一节中算法拼凑求解三维曲面函数的矩阵方程，并求解经过三维点云中所有三维点的三维曲面方程。
  • 在求解出曲面方程之后，就需要重建模型的三维网格。经典常用的方法自然是Marchcubes算法，即大名鼎鼎的MC算法，或者改进后的MD算法，这些都属于面绘制方法。而高端进阶一点同时需要高GPU算力的就是体绘制算法，其中会涉及到一点点光线追踪技术。
  • 如何使用MC算法去重建三维网格模型呢？首先需要将整个模型所占据的三维空间体素化，并求解每一个三维体素上8个顶点的曲面函数值。之后就是MC算法的经典步骤，大家可以去自行了解，当然，如果有需求可以在下方评论，如果人数较多我就会好好讲一讲MC算法。

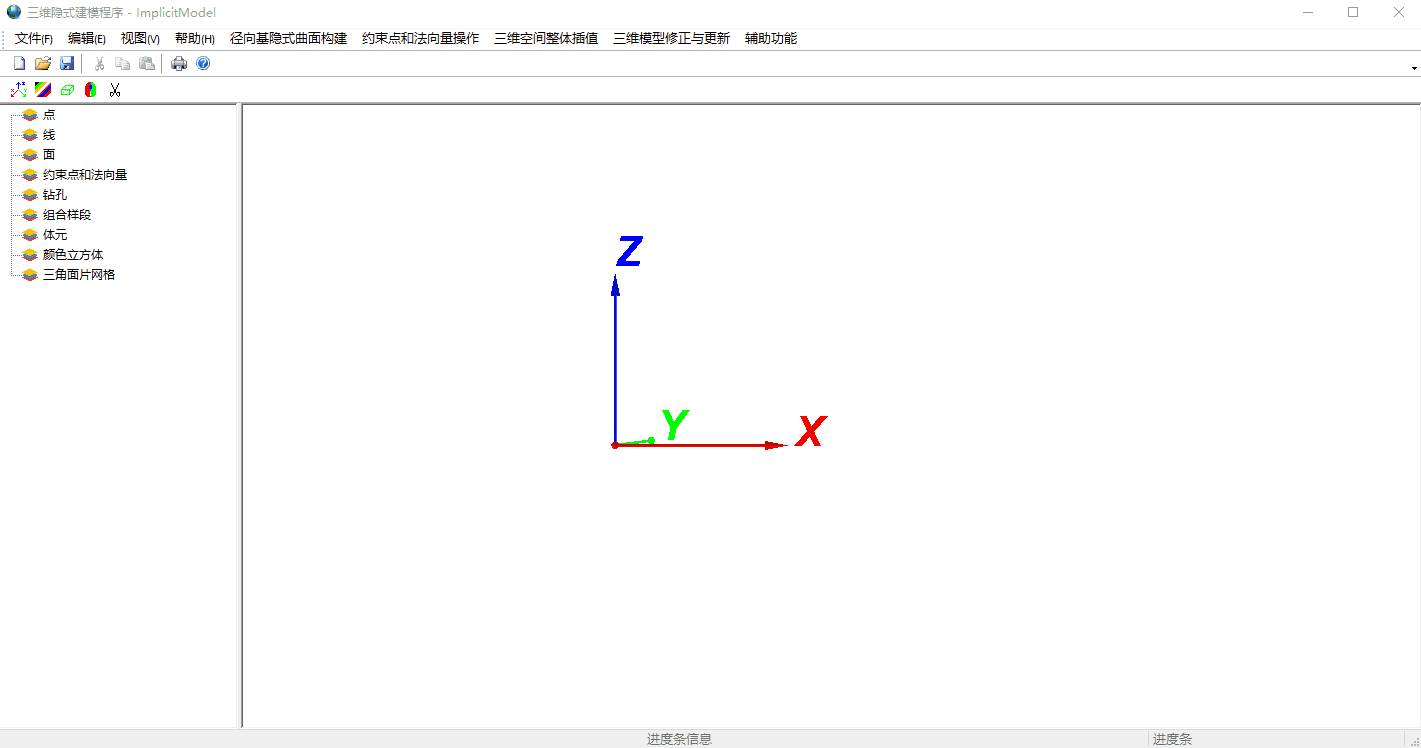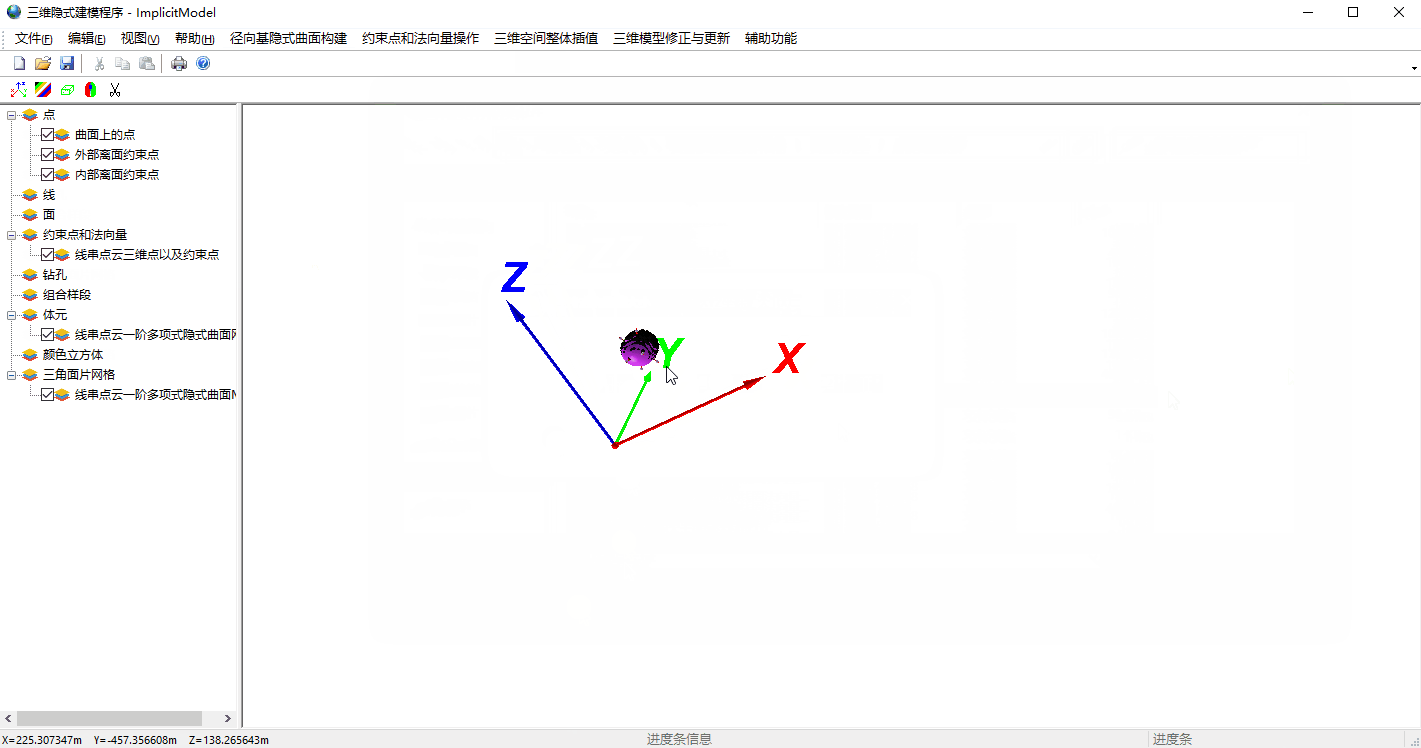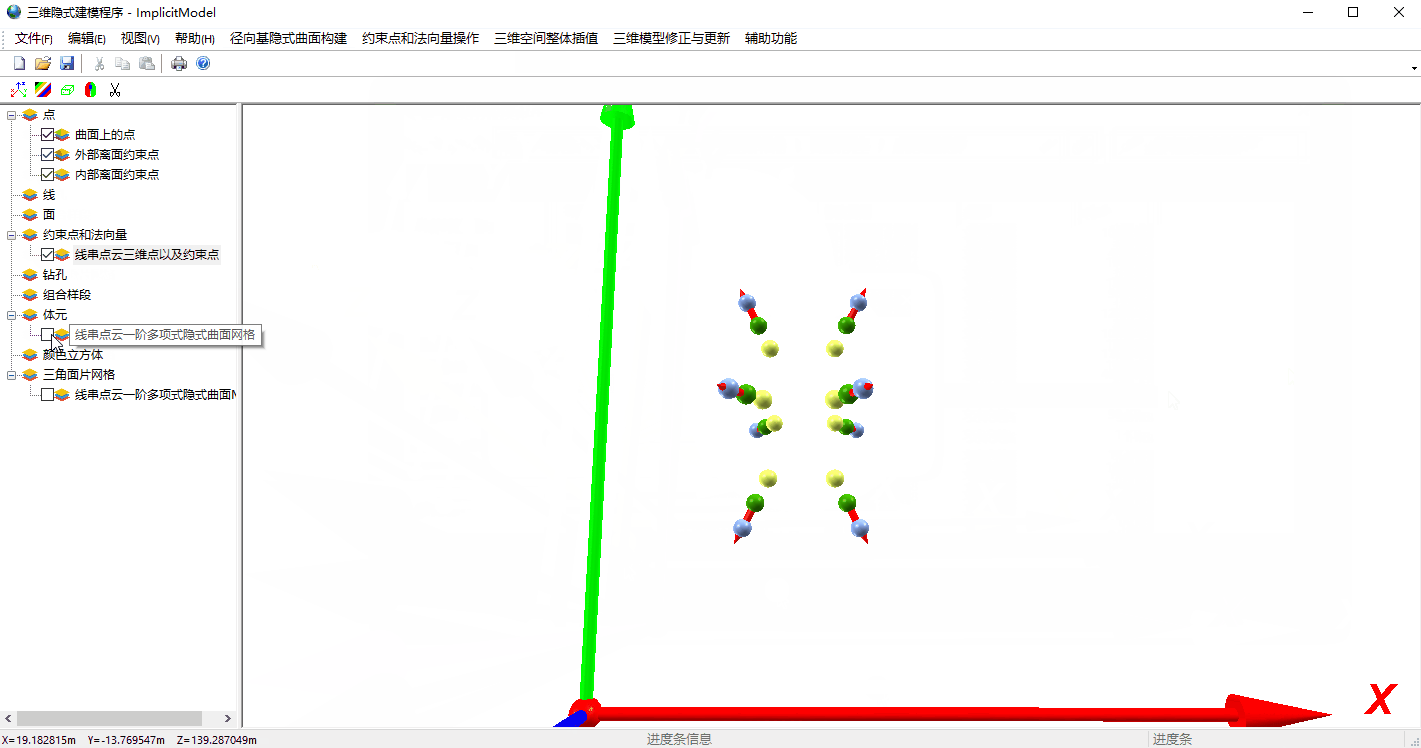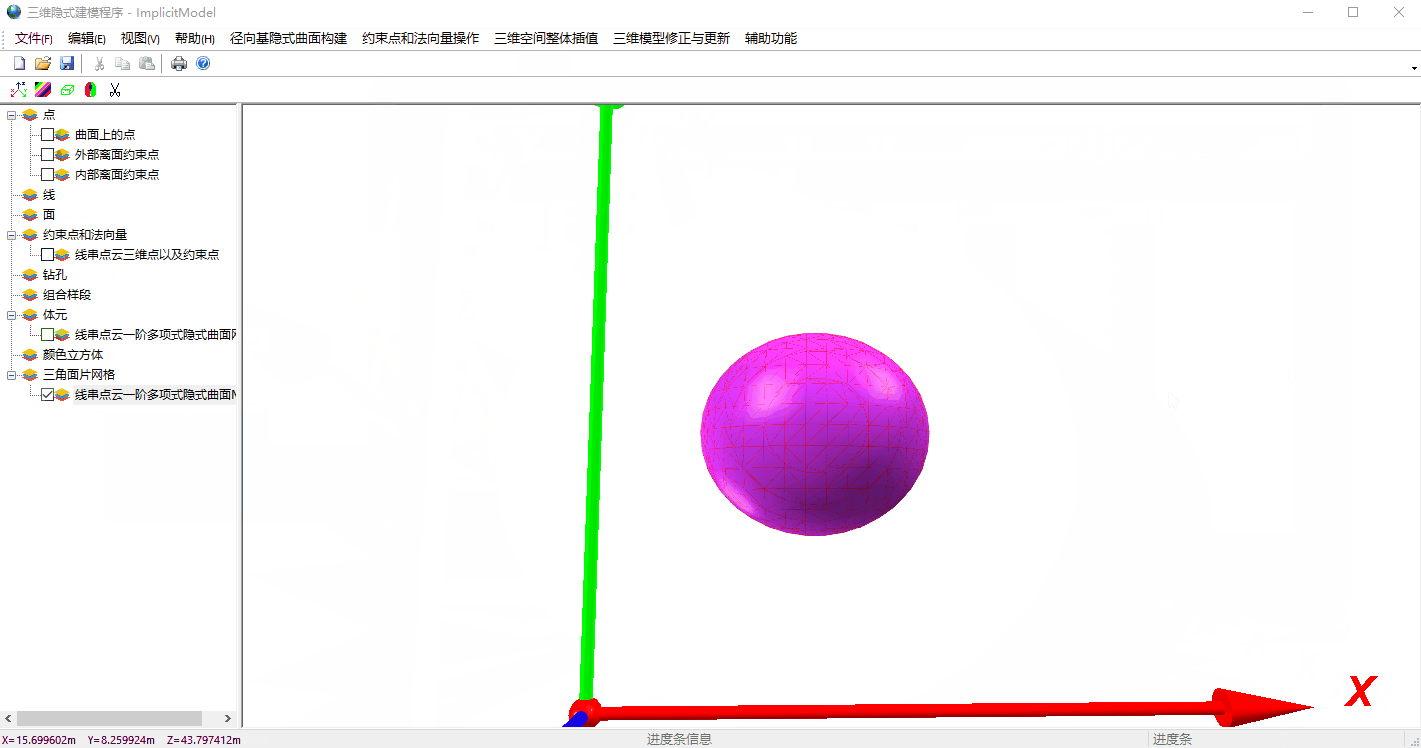
3 算法程序展示

这个程序中就是使用RBF三维重建算法以及MC算法对网格进行了重建，采用MFC+OpenGL搭建的程序框架。
三维点云重建 – 基于RBF的三维点云表面重建方法-StubbornHuang Blog

4 吐槽一下

Latex公式真的难写，写篇博客花了三个小时。